Projects

BARSElo: Player Rating System for Recreational Dodgeball
Samantha Pease

I built a machine learning system to estimate individual player skill in recreational dodgeball despite heavy team effects. Using ~790 historical games, I developed a Bradley-Terry model with Gaussian margin-of-victory extensions and Bayesian uncertainty for sparse-data players. The approach separates individual skill from team composition through batch optimization, validates predictions using both chronological and "new-team" evaluation modes, and achieves 56.8% accuracy on unseen team compositions. The interactive explorer features player skill trajectories, searchable databases, team comparisons, and model visualizations.

Trans Advice Agent
Samantha Pease

I built a retrieval-augmented QA system to surface community-sourced information about transgender healthcare. Users enter free-text questions and get concise, document-grounded summaries with links to the forum posts and resources that informed the answer; each response also includes a short confidence note. This is for information discovery, not medical advice.

Implementation highlights: semantic embeddings (all-MiniLM-L6-v2) stored in a FAISS index (IVFPQ) for memory-efficient nearest-neighbor retrieval, aggregation and summarization with Claude Haiku, orchestration and monitoring via LangChain/LangSmith, and a FastAPI backend deployed on Render. The index only contains public/community-contributed documents and the design emphasizes provenance and privacy. Future work focuses on broader curation, community evaluation, and bias/quality checks.

Instagram Network Analysis
Samantha Pease

This project explores the structure of an individual's Instagram social graph by identifying and analyzing mutual connections among followed users. I primarily looked at the data for my own Instagram network but also examined my sister's and roommate's networks for a comparison point. Future work would include comparing more diverse networks. The pipeline integrates web scraping and network science to uncover community structures, central users, and hidden patterns in online social behavior, and graph neural networks to predict potential future connections.

Cat Identification with Neural Network From Scratch
Sam Pease

I built a deep neural network from the ground up to explore how architecture, activation functions, learning rates, and other parameters affect performance. Starting with a small cat image dataset and later pivoting to a binary classification task using CIFAR-10 (Cat vs. Not Cat), I encountered firsthand the limitations of deep neural networks for image classification without convolutional layers. Despite experimenting with network depth and size, I found minimal accuracy gains—highlighting the importance of architecture over brute-force tuning. All training was done on CPU, further emphasizing hardware constraints in model development.

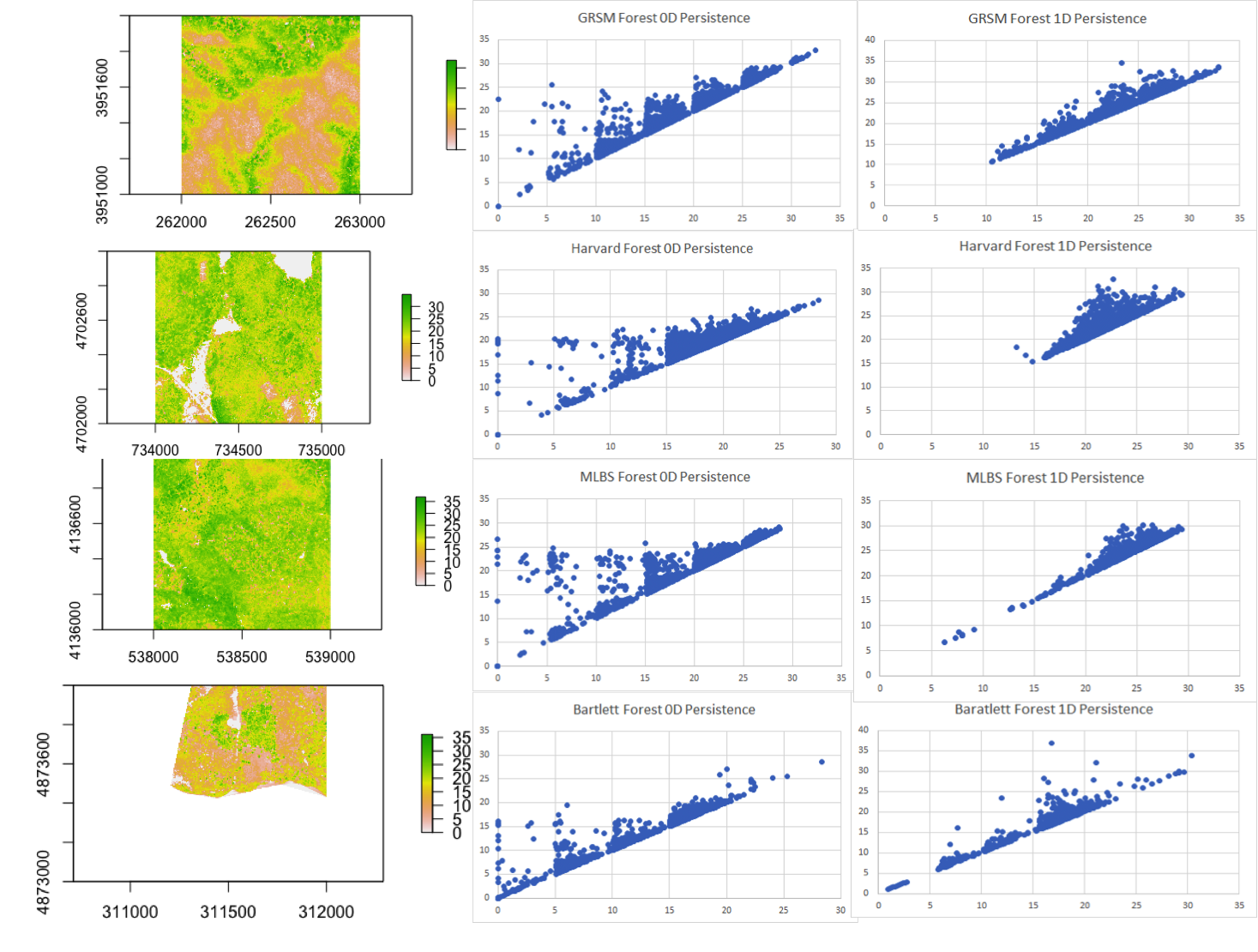
Topology as a Tool to Differentiate Canopy Architecture in North American Forests
Eva Arroyo, Sam Pease, Nikita Zemlevskiy

In this project, we used topological data analysis (TDA) to classify forest types based on LiDAR-derived canopy height models from four ecologically distinct U.S. forests. We extracted persistence diagrams—summaries of geometric features at multiple scales—using both 1D and 2D sublevel set filtrations, then transformed these into feature vectors for classification using support vector machines (SVM). Our results showed that 1D persistence, which captures broader structural trends in canopy architecture, outperformed 0D persistence in distinguishing between forest types. This work demonstrates how persistent homology can uncover meaningful ecological differences in complex spatial datasets.

Remote Wind Turbine Monitoring System
Sam Pease, Martin Cala

In the summer of 2017, I volunteered with WindAid, an international NGO based in Trujillo, Peru. I began by working in the engineering workshop, helping to construct a wind turbine (pictured below) for a rural home with no access to electricity. Later, another volunteer and I initiated R&D on a prototype monitoring system designed to remotely report windspeed, power generation, and battery capacity for installed turbines. The goal was to provide engineers with diagnostic feedback, as turbines were often located in remote areas and maintained by users with limited technical knowledge. We successfully developed a functional prototype and handed it off to WindAid’s permanent engineering team for continued development.